By Dave Pagurek, Austin Lee Slominski, Adam Ferriss
このチュートリアルでは、p5.jsを使用して3Dスケッチを作成するための新しい概念（x、y、zを含む）を紹介します。
まず、p5.jsでWebGLを使用するようにセットアップしましょう。createCanvas()の3番目のパラメータとしてWEBGLを渡します。
function setup() {
createCanvas(windowWidth, windowHeight, WEBGL);
describe('白い背景に赤い箱。');
}
function draw() {
background(255);
fill(255, 0, 0);
box();
}
3D座標空間
2Dスケッチでは、x軸とy軸を使用して水平方向と垂直方向の位置を定義します。3Dスケッチはこのモデルを拡張し、奥行きを定義するz軸を追加します。2Dで描画する場合、点(0,0)は画面の左上隅にあります。WebGLモードでは、スケッチの原点(0,0,0)は画面の中央にあります。デフォルトでは、x軸は左から右へ、y軸は上から下へ、z軸は奥から手前へ、つまり画面の「外側に向かって」伸びています。
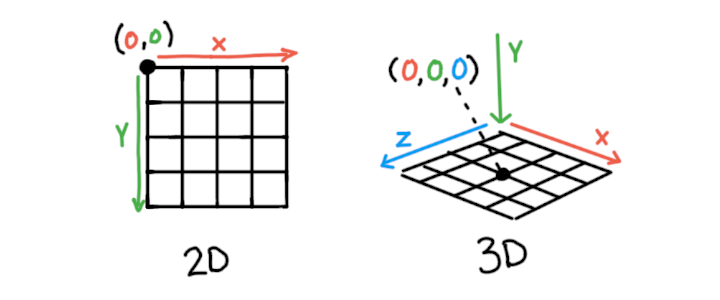
左側に2D座標系を示す図（左上に原点(0,0)がある）と、右側に3D座標系を示す図（中央に原点(0,0,0)がある）
setup()関数でdebugMode()を呼び出すと、x軸とz軸上のグリッドと、上の図のような赤緑青のx、y、z軸の矢印がスケッチに追加されます。
変換：3D形状の位置とサイズ
p5.jsには、3D空間内でオブジェクトを配置し向きを変える関数がいくつかあります：translate()、rotate()、scale()です。これらを総称してオブジェクトの変換と呼びます。これらのメソッドは2Dと3Dの両方の描画で利用できます。
translate()：空間内でオブジェクトを移動する
translate()は原点を指定された点に移動させます。translate()を呼び出した後に描画されるものは、すべてその点を基準に配置されます。translate()はx、y、z値の引数を受け取ります。上のスケッチのスライダーを使用して箱の平行移動を変更し、各軸に沿ってどのように移動するかを確認してください。以下のコードスニペットは、box()形状に対する単純な平行移動を示しています。
// 箱を右に100単位移動させる
translate(100,0,0);
box();
試してみよう！
ランダムウォークは、各ステップでランダムな方向に移動することを意味します。translate()を使用して3Dでランダムウォークを試してみましょう。各ステップの後にキューブを描画して、パンくずの軌跡のようにしてみてください！
rotate()：空間内でオブジェクトの向きを変える
rotate()は、その後に描画されるものの向きを変更します。
3Dでオブジェクトを回転させるためにいくつかの関数を使用できます。ほとんどの場合、rotateX()、rotateY()、rotateZ()のような関数を呼び出すのが最も簡単で、これらはそれぞれ特定の軸を中心に回転させることができます。各関数は回転角度を指定する単一の引数を受け取ります。上の例のスライダーを動かして、各軸での回転がどのように行われるかを確認してください。以下のコードは、これらのメソッドの使用例を示しています。
// X、Y、Z軸をそれぞれ45度回転させる
rotateX(QUARTER_PI);
rotateY(QUARTER_PI);
rotateZ(QUARTER_PI);
box();
デフォルトでは、p5.jsは角度をラジアンで期待します。ラジアンは0からTWO_PIまでの数値を使用して角度を指定します。度数を使用するには、radians(numberInDegrees)を使用して度数をラジアンに変換するか、angleMode(DEGREES)を使用します：
// 各軸を45度回転させる
rotateX(radians(45));
box();
// または
angleMode(DEGREES);
rotateY(45);
box();
また、rotate(angle, axis)を使用することもできます。これにより、2番目の引数としてベクトルを使用して回転させたい軸を指定できます。これにより、任意の軸を中心に形状を回転させることができます。以下の例では、マウス座標を使用して軸を作成し、その周りを回転させています：
scale()：空間内のサイズ
scale()は、その後に描画されるものの大きさを変更します。他の関数と同様に、x、y、z値の引数を受け取ります。
試してみよう！
キューブを上下に跳ねさせてみましょう。ただし、scale()を使用して、跳ねる際につぶれて伸びるようにして、漫画のような感じを出してみてください！
複数の形状の変換
変換関数は累積的で、その後に描画されるすべてのものに影響します。例えば、translate(50, 0, 0)を2回呼び出すと、それらは加算され、translate(100, 0, 0)を1回呼び出すのと同じになります。しかし、異なる形状を異なる変換で描画したい場合もあります。
push()関数は現在の変換とスタイル設定を保存します。その後、新しい変換を行った後、pop()関数を使用して元の変換に戻ります。結果として、push()とpop()の間で行われた変換やスタイルの変更は、そのコードの部分に限定されます。以下の例では、push()とpop()の間に変換を配置することで、それぞれ独自の位置に複数の箱を描画しています：
変換行列
これはより高度なトピックですが、これらの変換のそれぞれはモデル行列と呼ばれるものに影響します。モデル行列はビュー行列と投影行列と組み合わされ、これらはカメラのビューをシミュレートするのに役立ちます。この組み合わせが3Dシーンを生成します！ MDNでモデルビュー投影についてさらに学ぶことができます。
試してみよう！
別々に動かせる2つの球体を作ってみましょう。矢印キーで1つを、WASDキーでもう1つを制御できるようにしてみてください。
変換の順序が重要です！
変換が互いにどのように影響し合うかは、最初は予測不可能に感じるかもしれません。なぜなら、順序が重要だからです。各変換は常に次の変換に影響します。例えば、rotate()の後にtranslate()を呼び出すと、その平行移動の方向は回転の影響を受けます。座標系全体が回転し移動しているのであって、形状自体だけではありません。以下は、異なる変換順序のレシピで、使用できるものです。
デフォルト：シーン内のオブジェクトの配置
多くのオブジェクトを描画する場合、それぞれが独自の位置、向き、スケールを持つ可能性が高いです。このために、まずオブジェクトがあるべき中心にtranslate()し、次にその向きに合わせてrotate()し、最後にサイズに合わせてscale()します。これはデフォルトで使用するのに適した順序です。
試してみよう！
太陽系を作ってみましょう。各惑星が太陽の周りを独立して動き、それぞれが異なる速度で自転しているようにしてください！
ピボットポイントを中心に回転させる
時には、形状の中心ではない点を中心に回転させたいことがあります。これには、ピボットポイントにtranslate()し、必要に応じてrotate()またはscale()を行い、形状を描画する前に中心に戻るようにtranslate()します。以下のスケッチでは、この方法を使用して、形状の中心ではなく底面を基準にして押しつぶしたり引き伸ばしたりしています。
試してみよう！
腕を振るキャラクターを作ってみましょう！腕が体につながったままになるように、腕と体が接続する点を中心に回転させる必要があります。
対称性を持たせて描画する
時には、鏡像対称や回転対称性を持たせて同じものを複数回描画したいことがあります。このような場合、ループで描画することになります。各反復で、望む対称性の種類に応じてrotate()またはscale()を使用します。最後に、形状を描画するために必要な他の変換を適用します。
以下の例では、scale(-1, 1)を使用して水平方向の対称性を追加し、顔の目と耳を描画しています：
この例では、rotateY()を使用してストーンヘンジのシーンに回転対称性を持たせています。
試してみよう！
例の頭に、腕と脚のある体を追加してみましょう！
まとめ
3D座標を制御することで、より複雑な3Dシーンを作成できるようになります。この後に続くチュートリアルでは、これらのスキルを基に、変換後に描画するものをより細かく制御する方法を学びます。
用語集
GPU
GPU（Graphics Processing Unit）は、多くの計算を並列で実行するのに特に適したハードウェアで、3Dグラフィックスに強力な性能を発揮します。
モデル
ファイルから保存および読み込みができるカスタム3Dジオメトリ。
行列
ジオメトリの変換に関する情報を保持できる特殊な配列。
カメラ
3Dシーンの視点。
変換
ジオメトリのスケール、回転、平行移動を組み合わせたもの。動詞transformは、これらのプロパティを変更する際に使用されます。
頂点
x、y、z位置を持つ3D空間上の点。
面
固体の表面を作成する3つの点の集合。
